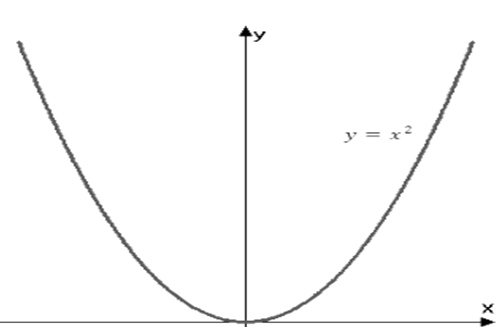
One of the applications of derivatives includes increasing and decreasing functions. To identify whether the given function is increasing or decreasing, the concept of derivatives is used.
An increasing function involves an increase in the value of y when there is an increase in the value of x. The curve moves in the upward direction. A decreasing function involves a decrease in the value of y when there is an increase in the value of x. The curve moves in the downward direction. When defined graphically, the increasing and decreasing functions in calculus are those functions which are moving in the upward and downward direction.
Others definitions of increasing and decreasing functions
1] For every x1 and x2 in an interval, a given function is said to be increasing when x1 < x2, f (x1) ≤ f (x2).
For every x1 and x2 in an interval, a given function is said to be strictly increasing when x1 < x2, f (x1) < f (x2).
2] For every x1 and x2 in an interval, a given function is said to be decreasing when x1 < x2, f (x1) ≥ f (x2).
For every x1 and x2 in an interval, a given function is said to be strictly decreasing when x1 < x2, f (x1) > f (x2).
Steps to determine whether a function is increasing or decreasing
The concept of first derivatives can be used to verify the type of functions given. It is assumed that the function f is continuous on [a, b] and differentiable on (a, b), then the following conditions hold good.
- The function is increasing in the interval [a, b] when f’ (x) > 0.
- The function is decreasing in the interval [a, b] when f’ (x) < 0.
- The function is constant in the interval [a, b] when f’ (x) = 0.
A function is said to be constant if the slope of the curve is 0 and is a horizontal line. An interval is the inclusion of all the numbers between two given numbers.
Steps to calculate the interval of increasing or decreasing functions
- The first derivative of the function has to be found.
- Find the value of x from the first derivative by the method of solving.
- Equate the first derivative to 0.
- After finding the values of x, form the open intervals and discontinuous points.
- Obtain a value from each interval and determine its sign from the first derivative.
- The function is increasing when f’ (x) > 0.
- The function is decreasing when f’ (x) < 0.
- Write down the intervals of increasing and decreasing functions.
Properties of monotonic functions
- Let f and g be two functions that are increasing (or decreasing) on the interval (a, b). The sum of the functions is also increasing (or decreasing) on the same interval.
- Suppose a function f is increasing (or decre asing) on the interval, then its opposite function – f is decreasing (or increasing) on the same interval.
- Suppose a function f is increasing (or decreasing) on the interval, then its inverse function 1 / f is decreasing (or increasing) on the same interval.
The above article talks about the concept of increasing and decreasing functions. This page answers the question – how do you find absolute min and max in calculus. To understand various concepts in calculus such as limits, differential calculus (differentiation), integral calculus (integration), multivariable calculus (function theory) please visit BYJU’s website.